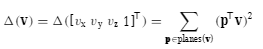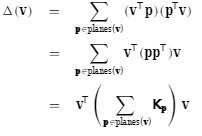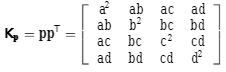xcsf's Blog

noooooooooooob

0%

QEM边折叠算法

发表于 更新于 分类于 ，

一、算法相关资料

算法来自论文：
Surface Simplification Using Quadric Error Metrics

通过计算网格图形上的每一条边的权重，每次移除最小权重的边。重复这个过程达到简化效果。

二、算法步骤

QEM算法步骤

  1. 初始化所有顶点的 Q 矩阵。
  2. 选择所有有效边。 (所有联通边 (v1, v2) 、或者长度小于某一个阈值的边。)
  3. 计算所有有效边的误差 ¯vT(Q1+ Q2)¯v 作为这条边的cost。
  4. 将所有的边按照cost的权值放到一个最小堆里。
  5. 每次移除最小的边，并且更新包含着v1的所有有效边的代价。

Q矩阵计算方法

基础知识平面方程(Plane Equation)

定义顶点的误差为顶点到该顶点相交的三角形的平面的距离平方和：

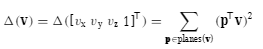
QEM距离平方和

  • 其中P为平面方程 [a,b,c,d]T , v为顶点[x,y,z,1]，法向量 n = [a,b,c]

  • (P·v)/|n| 为点v到平面P的距离

  • n模长等于1时，P·v即点到平面距离。

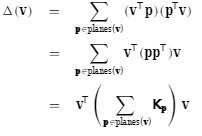
QEM距离平方和

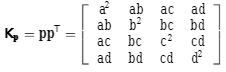
QEM矩阵Kp

这个基本二次误差Kp可以用来求空间中任意点到平面P的平方距离。我们可以把这些基本二次曲面加起来，用一个矩阵Q表示整个平面集合。

新顶点位置计算

  1. 选择v1 、v2、(v1+v2)/2中选择一个；

  2. 对二次项式Δ(v)求导，当求导等于0时；

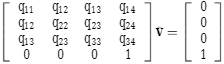
    QEM求导

    当左边矩阵可逆时，可求解：

    QEM可逆

    否则，根据第一条策略。

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
function calculatorEdgeDelta(geometry, edge) {
    let mat = new THREE.Matrix4()
    let deltaV = 0;
    //计算Q1+Q2
    let q1 = calculatorVertexDelta(geometry, edge.a).elements
    let q2 = calculatorVertexDelta(geometry, edge.b).elements
    mat.elements = q1.map((e, i) => {
        return e + q2[i]
    })
    edge.midv = calculatorVertexPos(geometry, edge)
    //计算vT (Q1+Q2) v 得到边的代价(cost)deltaV
    for (let j = 0; j < 4; j++) {
        let t = 0;
        for (let k = 0; k < 4; k++) {
            // console.log(edge.v.getComponent(k))
            t += edge.midv.getComponent(k) * mat.elements[j * 4 + k];
        }
        deltaV += t * edge.midv.getComponent(j)
    }
    edge.deltaV = deltaV
    return edge
}


//计算顶点Q矩阵
//传入一个顶点  找到与其关联的边 再找到 面  求Kp二次基本误差矩阵PTP之和Q 并返回 
function calculatorVertexDelta(geometry, vIndex) {
    let result = new THREE.Matrix4()
    result.elements[0] = 0
    result.elements[5] = 0
    result.elements[10] = 0
    result.elements[15] = 0
    let tmp = new THREE.Vector4()
    let f = findFaceWithVindex(geometry, vIndex)
    //找出与顶点vIndex关联的面 得到其平面方程[a,b,c,d] 计算Kp矩阵之和Q
    f.map(face => {
        //计算平面方程系数abcd 即 法向量(a,b,c)
        //d = -(ax+by+cz)
        let { x, y, z } = face.normal;
        let d = -geometry.vertices[face.a].dot(face.normal)
        tmp.set(x, y, z, d)
        for (let j = 0; j < 4; j++) {
            for (let k = 0; k < 4; k++) {
                result.elements[j * 4 + k] += tmp.getComponent(j) * tmp.getComponent(k);
            }
        }
    })
    return result;
}

效果

下图是使用three.js 实现QEM算法。对OBJ模型动态计算过程。可以看到对于简单模型，简化效果基本满足。经过多个模型测试，对于特殊形状模型简化容易出现破面现象。

QEM求导