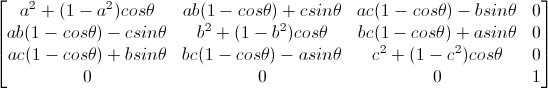一、了解模型矩阵、视图矩阵、投影矩阵
计算机在显示一个三维物体时,本质都是对相应的 顶点 坐标进行计算,进而渲染出图元、片元,得到显示屏上看到的结果。
而最原本的模型的各个顶点坐标并不是在世界坐标系中建立的(世界坐标系即下一节的球心坐标(ECEF))。以下称原本的模型坐标系为模型本体坐标系
那么我们需要将模型在世界坐标系下进行展示和运动,就得将模型所有顶点都转换到世界坐标系下。 这个转换过程可以用44的矩阵表示,称为*模型矩阵(Model Matrix)**。
现在模型通过模型矩阵转换成了世界坐标。需要用一个相机(Camera)来模拟人眼观测位置,因此,需要根据相机的位置和观察方位,将世界坐标系中的所有顶点(不只是模型)坐标转换为视图坐标系 (也称相机坐标系) 中的坐标,这个转换过程也可用44的矩阵表示,称为*视图矩阵(View Matrix)**
在视图坐标系中,所有的点都是三维的,最终要在显示器上展示。要将三维坐标投影到二维平面上去,这个44的矩阵表示,称为 *(透视)投影矩阵(Perspective projection Matrix)**
将模型顶点坐标与三个矩阵相乘后即得到屏幕(裁剪)坐标。
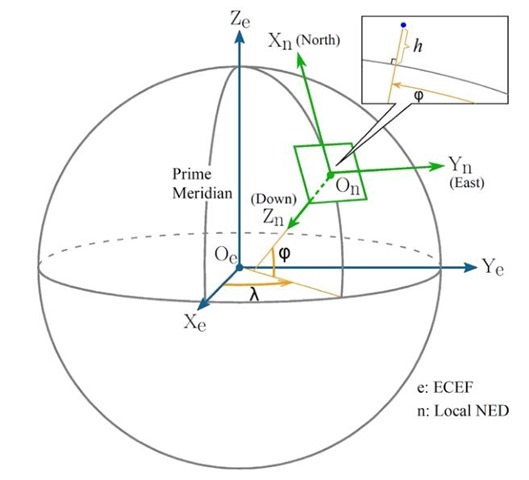
二、了解球心坐标(ECEF)与本地坐标(NEU)
本地坐标系(NEU): 一种地方空间直角系,原点为O,其北向坐标轴(N 坐标)为过O点的子午线的切线,指北为正。其东向坐标轴(E坐标)为过O点的椭球的平行圈的切线,指东为正。天顶向坐标轴(U坐标),为过O点垂直于N轴与E轴,指向天顶为正。
球心坐标系(ECEF,Earth-Centered,Earth-Fixed): 以地球为中心,坐标轴以International Reference Pole(IRM)和International Reference Meridian(IRM)为准,国际参考极点和国际参考子午线,遵照地表所确定。(earth-fixed)
三、平移、旋转、缩放
要用变换矩阵用来表示平移,需要将原本为(x,y,z)的点加上一维,即(x,y,z,w)这种四元组的方式来表达坐标,等同于三维坐标(x/w,y/w,z/w),称为 (齐次坐标)。
齐次坐标系使得我们可以在一中特殊的方程组中求出解,这个方程组中每一个方程都表示一个与系统中其他直线平行的直线。我们知道在欧几里得空间中,对这种方程组是无解的,因为他们没有交点。然而在现实世界中我们是可以看到两条平行线相交的。
规定(x, y, z, 0)表示一个向量,(x, y, z, 1)或(x’, y’, z’, 2)等w不为0时来表示点。
对于平移变换矩阵: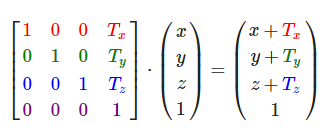
对于X旋转变换矩阵:
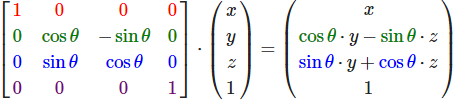
对于Y旋转变换矩阵:
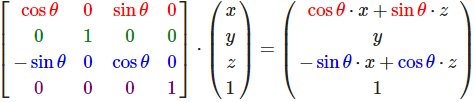
对于Z旋转变换矩阵:
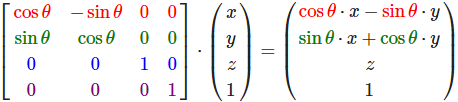
对于缩放变换矩阵:
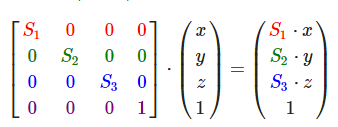
对于任意轴旋转:
首先将旋转轴平移至与坐标轴重合,然后进行旋转,最后再平移回去。
第一步平移
很简单,坐标做减法就可以得出。
第二步旋转
将向量旋转至与Z轴重合。即先绕X轴转角度为α;再绕Y轴旋转至与Z轴重合,旋转的角度为-β。
绕Z轴旋转角度θ
第三步
反向旋转平移回去,得到结果。即绕Y轴旋转角度为β;绕X轴转角度为-α;反向平移。
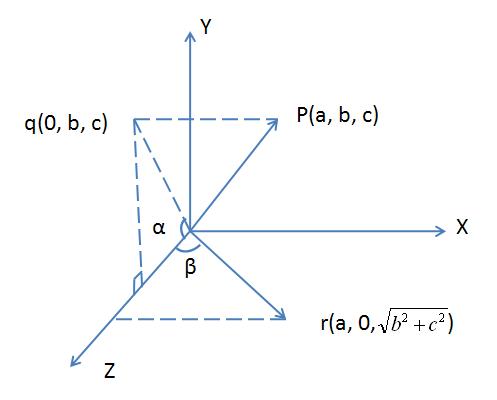
如果不需要平移,最终结果公式为: